In 1852 a South African mathematician asked a seemingly simple question that triggered endless dispute, left a trail of overturned publications in its wake and culminated in a resolution that has stretched the very tenets of math.
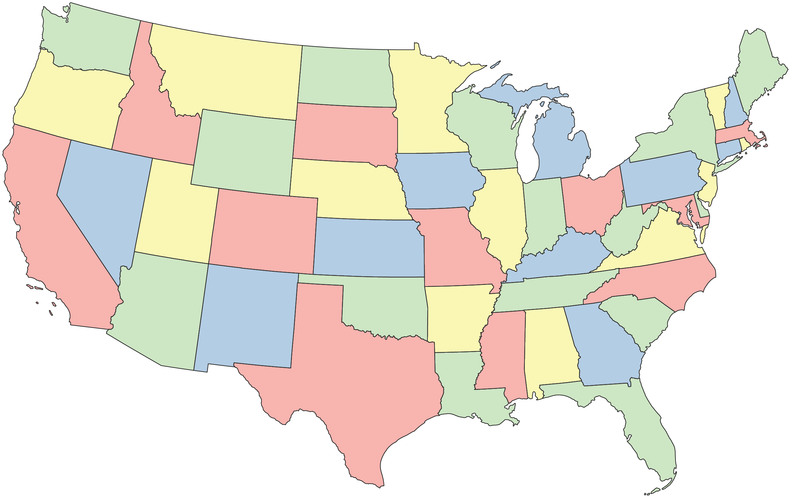
The color conundrum that stirred up so much trouble: What is the fewest number of colors needed to color a map so that no neighboring states or other designated areas have the same hue? Here’s how it works. Check out the map of the contiguous U.S. below.
Credit: June Kim
It looks a little bare-bones. To make maps more vivid and clearly highlight their borders, cartographers tend to color in the regions like so:
Credit: June Kim
Naturally, we don’t want neighboring states to have the same color, because that would make the boundaries more confusing. Under this constraint, we used four colors to fill in the map above. Could we have done it with only three? Might other maps require five or six?
The map doesn’t need to correspond to real geography—any partitioning of a flat surface into distinct regions qualifies. The question is, given any such map, what is the minimum number of colors required to fill in each region so that no two adjacent regions have the same color? Some ground rules: each region must be contiguous, so technically Michigan violates the setup because Lake Michigan severs the state into two disconnected parts. For two regions to count as adjacent, they must share some contiguous border; touching at a single point (or discrete set of points) doesn’t qualify. For example, Utah and New Mexico famously only touch at a corner and so do not count as neighbors for our purposes.
With the rules established, here are some questions with surprising answers. Suppose I printed out a large poster with a complicated map containing a few thousand regions. How long would it take you to determine whether the map could be colored with two colors? Three colors? Four colors? You don’t necessarily need to find a coloring, just decide whether a coloring exists for each number of colors. Curiously, while these three tasks seem nearly identical, they each require radically different amounts of time to complete. Using the best-known methods:
- Deciding whether two colors suffice would take about an hour. To do it, pick out any region and choose a color for it, say, red. This forces all of the region’s neighbors into the other color, say, blue. In turn, all of their neighbors become red, and so on, propagating through the map. Eventually you either encounter a conflict where neighboring regions share a color, in which case no “two-coloring” exists, or the colors spread through the whole map conflict-free, in which case you’ve found a valid coloring. A back-of-the-envelope calculation with 3,000 regions at a rate of 1 second per coloring yields 50 minutes of time well spent.
- Suppose the map can’t be filled with only two colors. Deciding whether three colors suffice would take longer. The afternoon would pass you by. The weeks would peel off the calendar as you furiously scribbled endless configurations, searching for one that works. To carry forth, you’d have to pass down the ongoing task to your children and they to their children. Generations of lives devoted to nothing other than finding a three-coloring of this map wouldn’t put a dent in the workload as the sun inevitably engulfs the Earth in some billions of years and puts an end to the silly endeavor, leaving us barely closer to an answer. Determining whether an arbitrary map has a three-coloring is hard. Here “hard” is a technical term indicating that it falls into a class of computational problems renowned for their time-consuming difficulty called NP-complete problems. For problems in this class, we don’t know any faster methods than more or less brute-force searching through every possible solution. That search space grows exponentially as the size of the problem increases. For a small map with only a few regions, we could afford to exhaustively look through every possible three-coloring until we find one that works (or conclude that there isn’t one). But the number of ways to assign three colors to maps with thousands of regions is so astronomical that it renders exhaustive search hopeless.
- And four colors? Well, that takes about one second or the time you need to say “yes,” because every map can be colored with four colors. This is the infamous and long-disputed four-color theorem.
Francis Guthrie first conjectured the four-color theorem in 1852 when he noticed that the counties of England only needed four colors to properly fill. He suspected this rule would generalize to any map, but although any kindergartner could understand the question, neither he nor his colleagues could prove it. It was clear that three colors wouldn’t always hack it, as evidenced by the diagram below, where every region neighbors every other one.
Credit: June Kim
But nobody could find a map that required five colors. Stymied by the problem, famed mathematician Augustus De Morgan grew obsessed and concluded that a new axiom—which in math is a statement that’s assumed to be true without proof, from which more complicated statements can be derived—must be added to the foundations of math to resolve Guthrie’s conjecture.
The fevered frustration ostensibly ended in 1879, when a proof emerged that four colors always suffice. This was underscored by a second independent proof a year later. With the matter settled and accolades distributed, captivated mathematicians returned to their normal research programs. Except for some. Eleven years after the publication of the first proof, both proofs were overturned and the slippery four-color theorem reverted its status back to the four-color conjecture. Percy Heawood, who exposed a hole in the original proof, did make some progress, though, by proving that five colors always suffice for filling any map. This left the math world in a rather embarrassing position. A problem so seemingly simple had one of two answers—four or five—but nobody knew which. It would stand this way for almost a century more.
Nobody could find a map requiring five colors, but ruling out the possibility of one altogether remained elusive. Because there are an infinite number of maps, one could never check each of them individually. A key technique toward a solution involved reducing the problem to a finite set of cases that could be checked individually. The leap from infinite to finite seems vast, but the monstrous number of cases to check still far exceeded what any person could manually process. So mathematicians Kenneth Appel and Wolfgang Haken turned to a daring idea: program a computer to process them instead. In 1976, after years of fine-tuning and over a thousand hours of computer time, their algorithm finished exhaustively checking every case and the four-color theorem was established. It was the first major theorem to use a computer in its proof.
The math world lit ablaze with equal parts celebration and dismay. One of Appel and Haken’s colleagues, Bill Tutte, rejoiced that they “Smote the Kraken,” while others despised the thought of computers encroaching on human ingenuity. The affair also posed a philosophical problem in the math community. Does a proof that can’t be verified by humans count as a proof at all? Many expected the work to eventually be retracted, like both of the alleged proofs that preceded it. The New York Times even refused to report on the announcement at first because proofs of the four-color theorem “were all false anyway.”
Multiple attempts to refute the computer-assisted proof failed in the following decades. Mathematicians have since drastically simplified the proof and verified the computer code, but to this day, no proof of the theorem without the aid of computers is known. The four-color theorem is now widely accepted as a fact, but still a yearning lingers over it. A computer program that systematically analyzes reams of configurations doesn’t explain exactly why every map can be filled with four colors. Although mathematicians now welcome computers as partners in discovery, they still search today for a more illuminating proof of this colorful puzzle.
This is an opinion and analysis article, and the views expressed by the author or authors are not necessarily those of Scientific American.